Molecular Crystals
Molecular crystals are a class of solids comprising molecular building blocks bound by van der Waals (vdW) interactions. They are used as functional materials for various applications, including organic electronics and photovoltaics, non-linear optics, and primarily pharmaceuticals because most drugs are marketed as solid forms of the active ingredient. Owing to the weak nature of vdW interactions, the same molecule may crystallize in several different structures, known as polymorphs. Polymorphs may be very close in energy and yet possess markedly different physical and chemical properties. For device applications, crystal structure may affect the electronic and optical properties. For pharmaceuticals, the crystal may affect the dissolution rate and thus the drug bioavailability. The ability to predict all the possible polymorphs of a particular molecule and their properties is therefore critically important. Molecular crystal structure prediction is extremely challenging because it requires searching a high-dimensional space with quantum mechanical accuracy. To predict the structure of molecular crystals we develop the genetic algorithm (GA) code, GAtor, and its associated structure generation package, Genarris.
Genarris: a random structure generator for molecular crystals
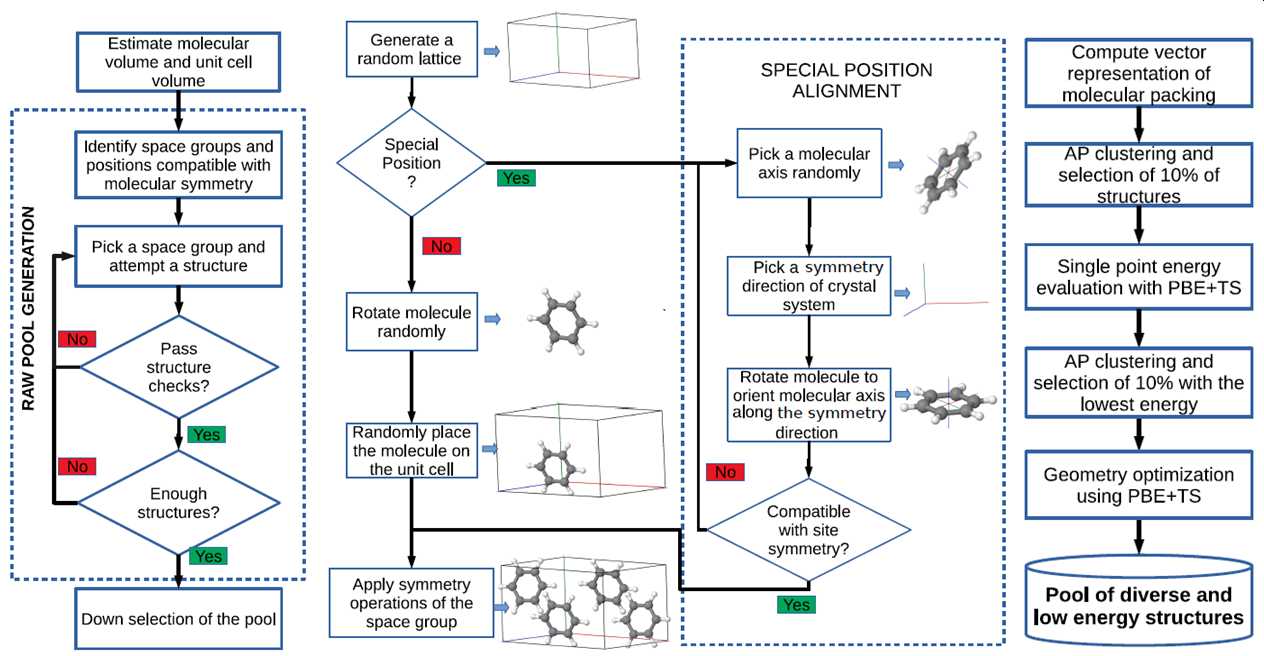
Genarris is a random structure generator for molecular crystals, which can be used for seeding crystal structure prediction algorithms, for generating datasets to train machine learning models, or for crystal structure prediction by random sampling. MPI-based parallelization facilitates the seamless sequential execution of user-defined workflows. The workflow of Genarris is illustrated below. Genarris starts by estimating the the unit cell volume based on the single molecule structure, using a machine-learned model trained on experimental structures. Then, structures are generated in all space groups compatible with the molecular point group symmetry and the requested number of molecules per unit cell, including space groups with molecules occupying special Wyckoff positions. A hierarchical structure check procedure detects unphysical close contacts efficiently and accurately. Special intermolecular distance settings have been implemented for strong hydrogen bonds. Once a “raw pool” is generated, down-selection may be performed by executing user-defined sequences of clustering and selection based on energy and/or diversity considerations.
Computer Physics Communications, 250, 107170 (2020); The Journal of chemical physics 148, 241701 (2018)
GAtor: a massively parallel genetic algorithm (GA) for molecular crystal structure prediction
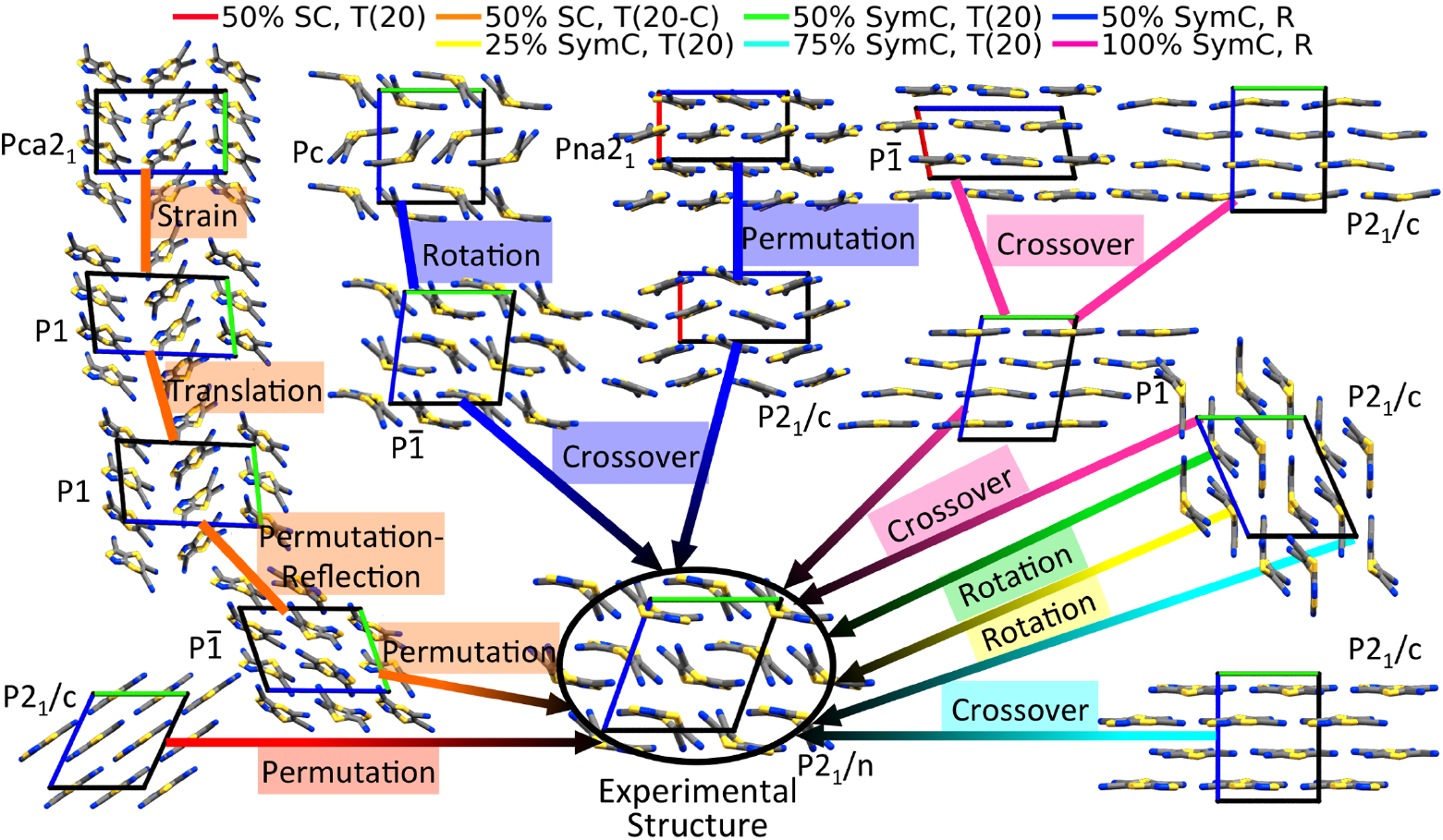
GAs rely on the evolutionary principle of survival of the fittest to perform global optimization. The target property is mapped onto a fitness function and structures with a high fitness have an increased probability to “mate” and propagate their structural “genes”. The process repeats iteratively until an optimum is found. GAtor has three special features: A variety of crossover and mutation operators, designed for molecular crystals, balance exploration and exploitation by breaking or preserving space group symmetries; Evolutionary niching helps overcome initial pool bias and selection bias; Massive parallelization is achieve by spawning several GA instances that only interact through a shared population. The recommended best practice for crystal structure prediction is to run GAtor several times with different settings. The figure below demonstrates how the experimental structure of tricyano-1,4-dithiino[c]-isothiazole (TCS3) was generated in seven GAtor runs with different settings via different evolutionary routes, starting from initial pool structures.
Finding Tetracene Polymorphs with Enhanced Singlet Fission Performance by Property-Based Genetic Algorithm Optimization
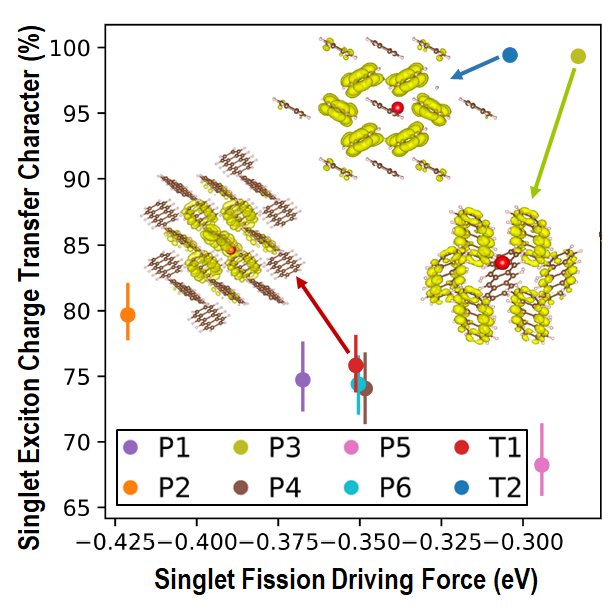
The efficiency of solar cells may be improved by using singlet fission (SF), where one singlet exciton splits into two triplet excitons, to generate two charge carriers from one high-energy photon. SF occurs in molecular crystals. SF performance (rate and triplet yield) depends on the crystal structure. Tetracene is a quintessential SF material. In the common form of tetracene (labeled T1), SF is experimentally known to be slightly endoergic. This means that modifying the crystal packing may potentially shift the singlet and triplet excitation energies to make SF more favorable. Indeed, a second, metastable polymorph of tetracene (labeled T2) has been experimentally found to exhibit better SF performance. We set out to investigate whether an even better form of tetracene for SF could be found.
To this end, we implemented in GAtor a fitness function tailored to simultaneously optimize the SF rate and the structure’s stability. The property-based GA successfully generated more structures predicted to have higher SF rates and provided insight on packing motifs associated with improved SF performance. We discovered a putative polymorph (labeled P3), predicted to have superior SF performance to the two known forms of tetracene. This structure has a higher thermodynamic driving force for SF than both known forms of tetracene, and a singlet exciton with a high degree of charge transfer character. It is only 1.5 kJ/mol higher in energy than the common form of tetracene, well within the viable polymorph range. Therefore, it may be experimentally synthesizable.
Crystal Structure Prediction of Energetic Materials
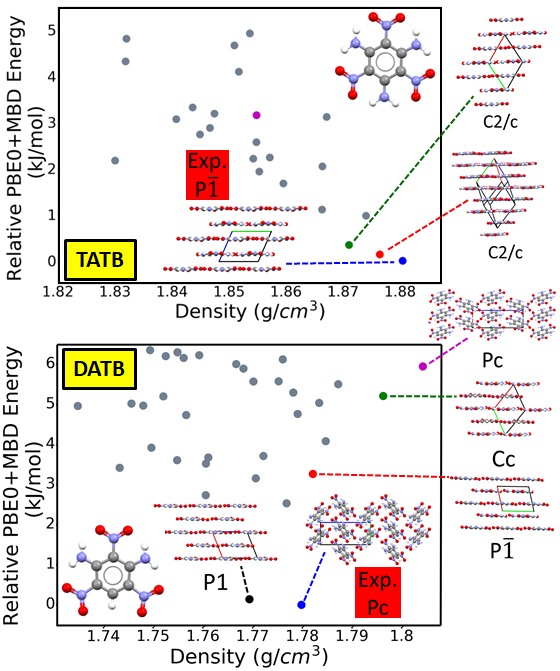
Energetic materials (EMs), including propellants and explosives, have a broad range of military and industrial applications. EMs have an inherent trade-off between energy and safety. Most EMs either exhibit high explosive power or low sensitivity to external stimuli, including thermal conditions, impact, shock, friction, transit, and light. Because most EMs release energy stored in chemical bonds during a combustion reaction, insensitive EMs that are thermally stable and resistant to shock typically have low explosive power. EMs are often deployed in the form of molecular crystals. Hence, their key properties are heavily dependent on the crystal structure. The crystal density is an important property because it determines the amount of energy stored per volume of material. Layered packing motifs are correlated with low sensitivity. Therefore, dense layered crystal structures are desirable for EMs.
EM crystals are denser than typical molecular crystals and are characterized by unique intermolecular interactions between multiple nitrogen-containing chemical groups. Therefore, they present a challenge for crystal structure prediction and for the dispersion-inclusive density functional theory (DFT) methods often used for ranking putative structures. The TATB and DATB energetic compounds, shown here, only differ by one amine group. This small difference in the molecular structure gives rise to significantly different potential energy landscape. For TATB stability is correlated with density and layered packing motifs are favored. For DATB, several putative structures are denser than the experimentally known structure but higher in energy. The experimental structure of DATB, and several putative structures, have a herringbone packing motif. We have found a putative polymorph, which is very close in energy to the experimental structure and has a more desirable layered packing motif.
CrystEngComm, 23, 6023 (2021); J. Chem. Theory Comput. 18, 4456 (2022)
A machine learned model for molecular crystal volume estimation
The first step in a crystal structure prediction workflow is to estimate the volume of the molecular crystal based on the single molecule’s structure to define the search space. To this end, we have developed a machine learned (ML) model. The success of ML models for physical systems hinges on a good choice of descriptors that represent the salient features of the systems being studied. Our model is based on two descriptors: the volume enclosed by the packing-accessible surface and molecular topological fragments. The volume enclosed by the packing-accessible surface accounts for the presence of voids and sterically hindered regions, as well as for the effect of conformational changes. The molecular topological fragments are capture the bonding environments of the atoms in the molecule and the inter-molecular interactions they may form. the model is trained on a data extracted from the Cambridge Structural Database (CSD). Including both geometric and chemical features produces an accurate model with robust performance for unseen data.

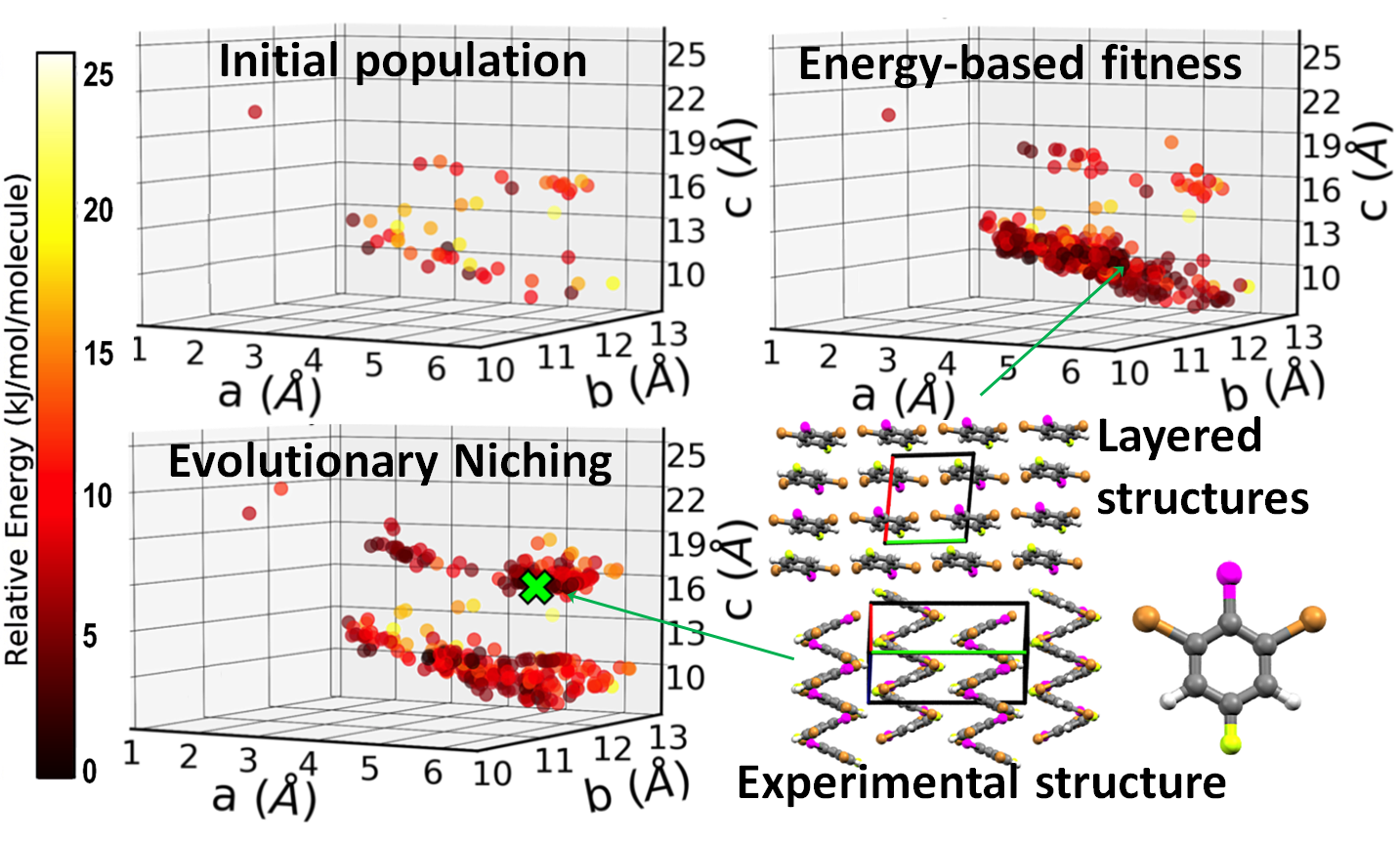
Evolutionary niching in GAtor
Typically, genetic algorithms for crystal structure prediction use an energy-based fitness function, which assigns a higher fitness to structures with lower energy. In addition to energy-based fitness, evolutionary niching has been implemented in GAtor to perform multimodal optimization by simultaneously evolving several sub-populations. Machine learning is used to dynamically cluster the population by structural similarity. A cluster-based fitness function is then used to steer the GA towards promising under-sampled regions of the configuration space. This reduces initial population and selection biases (evolutionary drift) and improves the GA performance. An example is shown here for 1,3-dibromo-2-chloro-5-fluorobenzene. Energy-based fitness preferentially samples a basin that contains layered structures. Evolutionary niching enhances sampling in the region of the experimental structure, which has a zigzag packing motif.